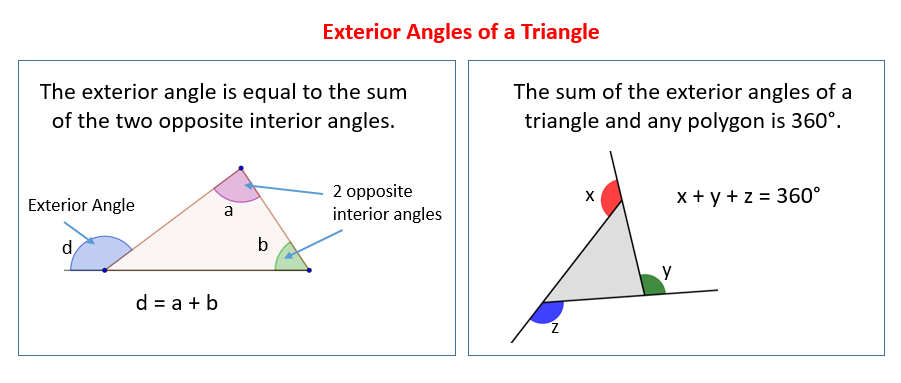
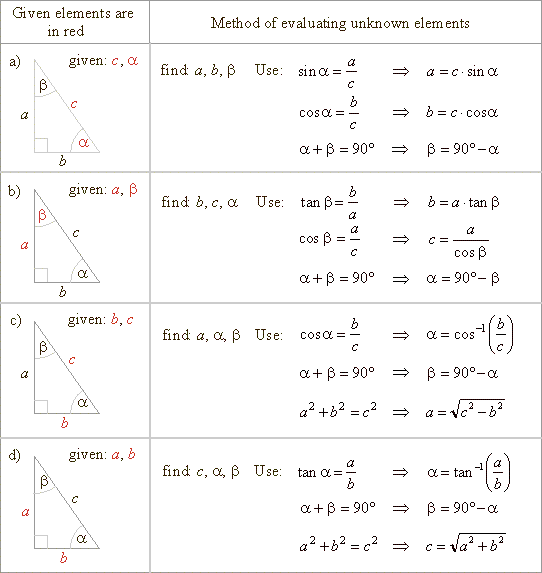A) The Angles of 1:2:√5 Triangle in terms of Golden Ratio, (B) The

Download scientific diagram | (A) The Angles of 1:2:√5 Triangle in terms of Golden Ratio, (B) The Side Lengths of 1:2:√5 Triangle in terms of Golden Ratio from publication: Metallic Means and Right Triangles: The Geometric Substantiation of all Metallic Ratios | This paper introduces certain new geometric aspects of the Metallic Ratios. Each Metallic Ratio is observed to be closely associated with a special right triangle, which provides the precise fractional expression of that Metallic Ratio. This work explicates the geometric | Geometrics, Fractionation and Work | ResearchGate, the professional network for scientists.

Special Right Triangles: Types, Formulas, Examples - Turito

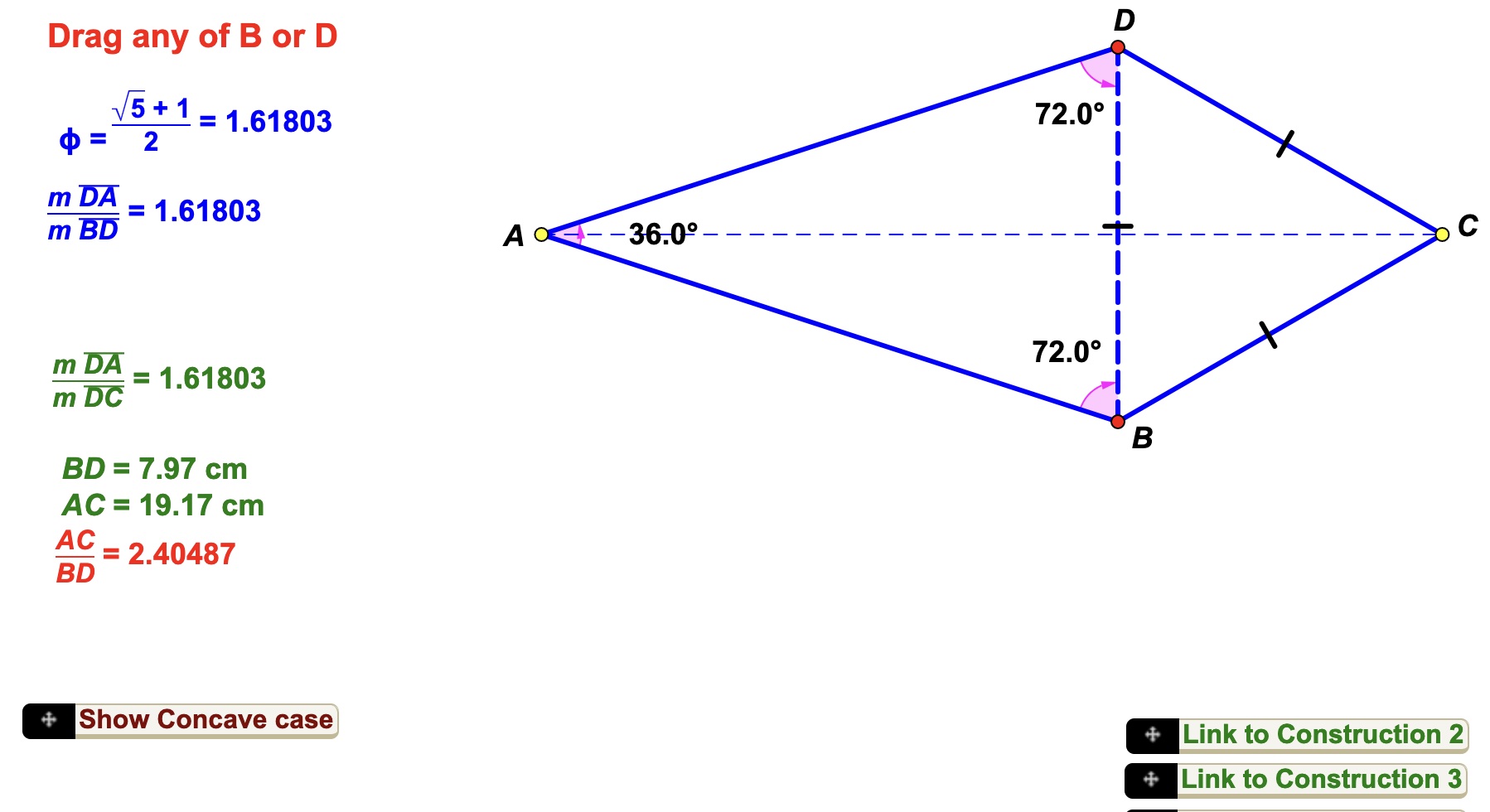
Golden Quadrilaterals

Article 56: Geometry - The Golden Ratio - Part 1 - Introduction - Cosmic Core

lengths of sides in golden ratio isosceles triangles - Mathematics Stack Exchange

geometry - Is the angle of the 345 triangle (pythagorean triple) related to the Geometric Progression. 4, 2, 1, 1/2, 1/4? - Mathematics Stack Exchange

Irrational number - Wikipedia

Golden Ratio - FasterCapital

THE GOLDEN RATIO

cdn1./wp-content/uploads/2021/12/golden-r

Pythagoras Theorem and Its Applications

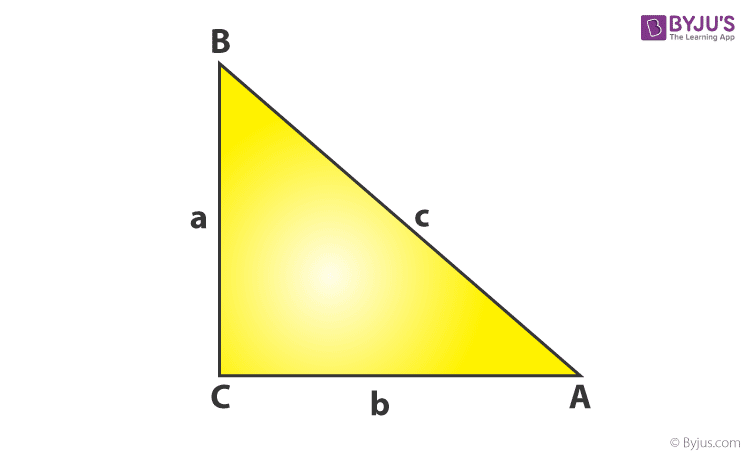
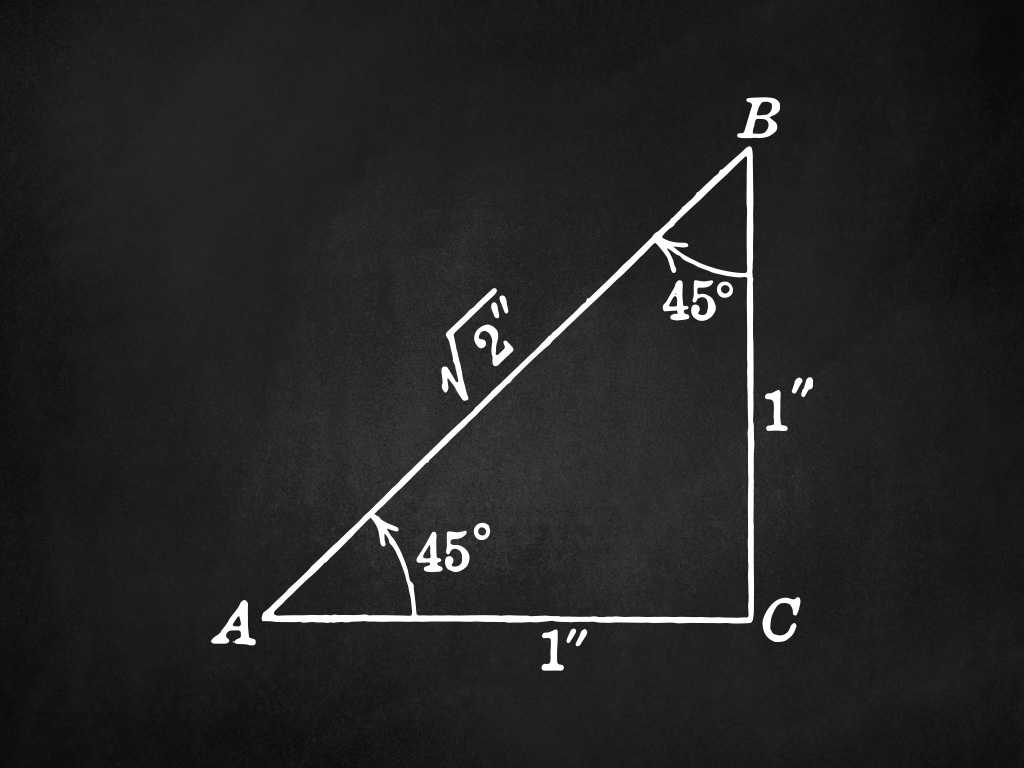
Right Angled Triangle (Definition, Properties, Formulas)

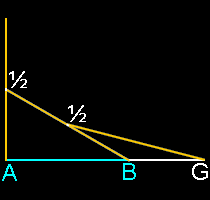
Phi, the Golden Ratio and Geometry

Golden ratio - Wikipedia