Why the proof of closure under addition in Linear Map is $(T+S)(u+v)$ instead of $(T+S)(u)$ and $(T)(u+v)$? - Mathematics Stack Exchange

I am reading Linear Algebra Done Right and want to prove that $L(V, W)$ is a vector space. I have read the solution here: Why the proof of closure under addition in Linear Map is $(T+S)(u+v)$ inst

How to Prove a Set is Not Closed Under Vector Addition

Dynamics of the optimality control of transmission of infectious disease: a sensitivity analysis

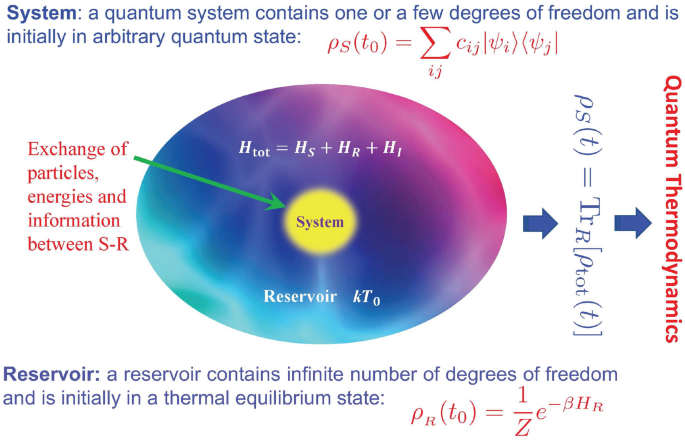
Quantum thermodynamics of single particle systems

Reproducing kernel Hilbert space - Wikipedia

Convolution - Wikipedia

Solved True or False a. If u and v are nonzero vectors with

Phase patterning of liquid crystal elastomers by laser-induced dynamic crosslinking

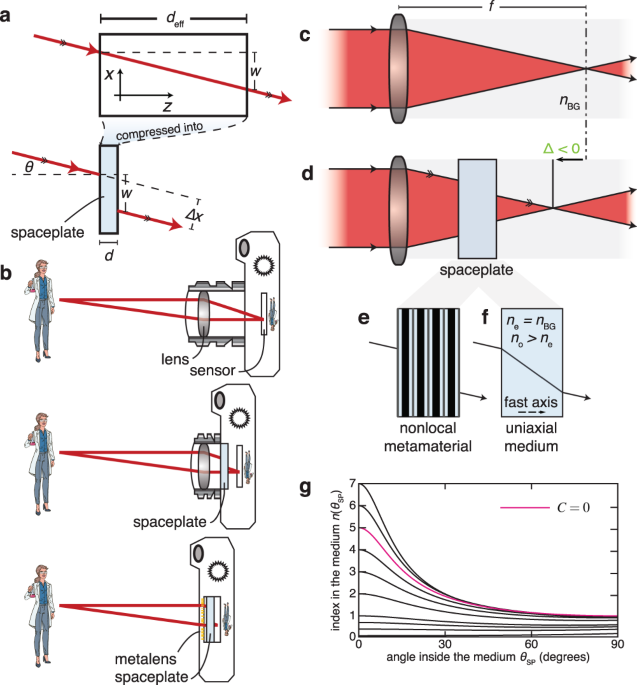
An optic to replace space and its application towards ultra-thin

Solved Let T: R^2 rightarrow R^2 be a linear transformation

Transpose - Wikipedia

Permutation matrix - Wikipedia

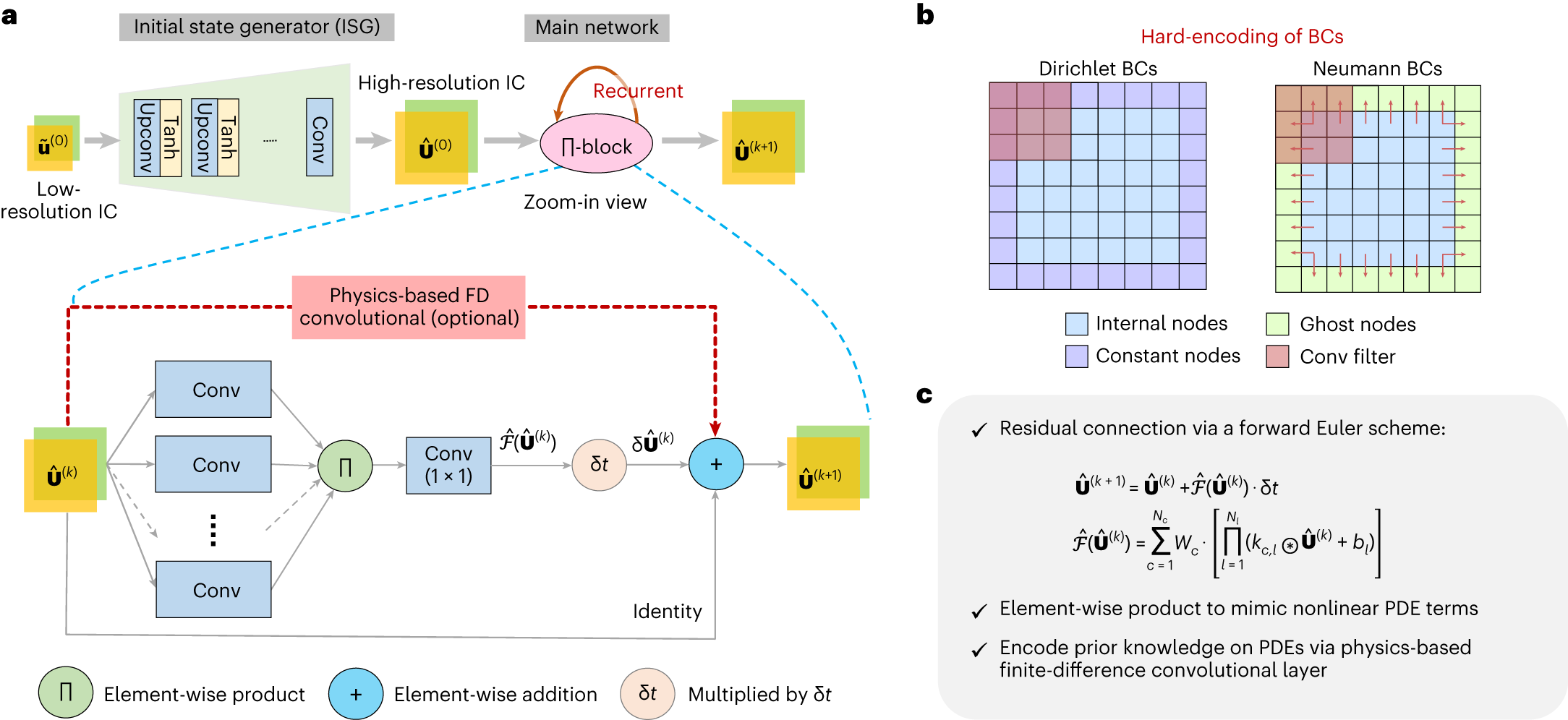
Encoding physics to learn reaction–diffusion processes

Solved How do you prove whether a S is closed under vector

T:V ightarrow W$ be a linear map and $v_1v_n$ be basis for $V